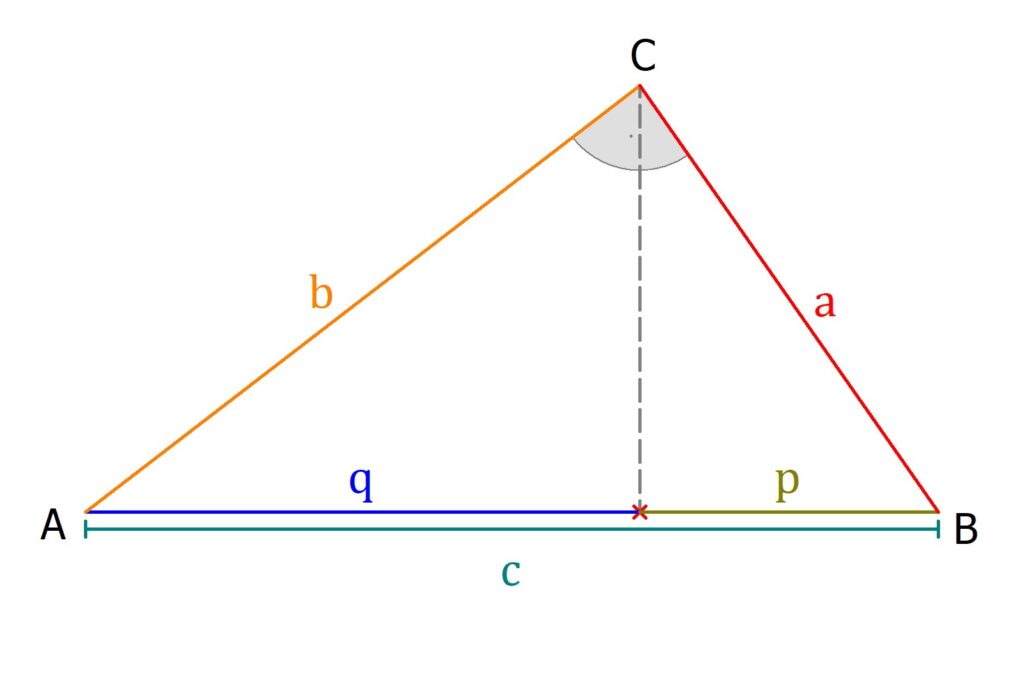
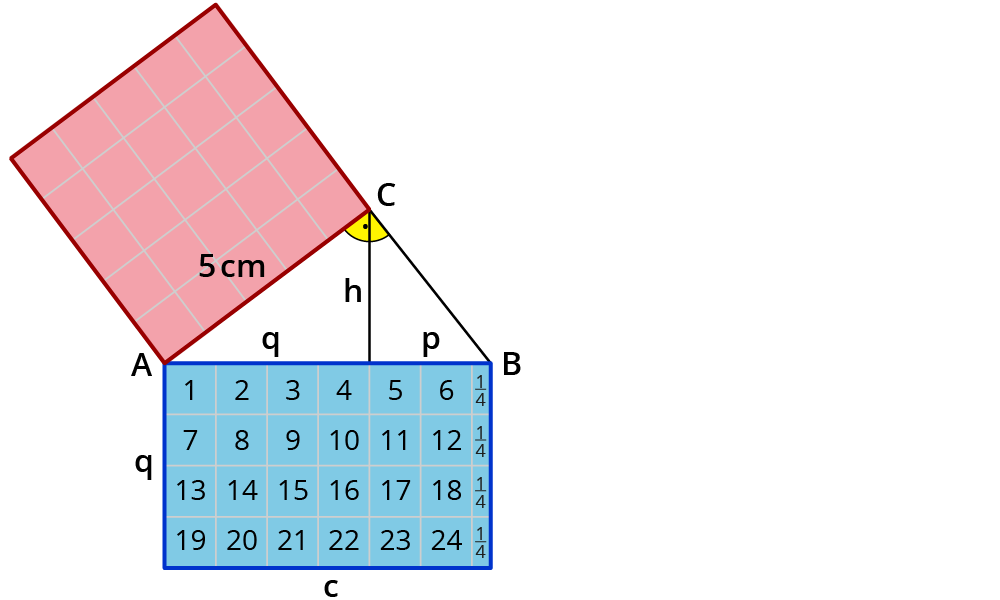
Der Kathetensatz besagt, dass gilt:
- a² = p · c.
- b² = q · c.
Anwendungsgebiete. Der Kathetensatz wird hauptsächlich in folgenden Fällen angewendet: Berechnung von Streckenlängen in einem rechtwinkligen Dreieck. Konstruktion eines Quadrats mit demselben Flächeninhalt wie ein gegebenes Rechteck.Der Kathetensatz des Euklid
Mit Hilfe des Kathetensatzes kannst du die Längen in einem rechtwinkligen Dreieck berechnen. Länge des Hypotenusenabschnitts p (in cm): Nach dem Kathetensatz gilt p·c=a2Du stellst nach p um und setzt 12 für a und 15 für c ein. c ist die Hypotenuse.
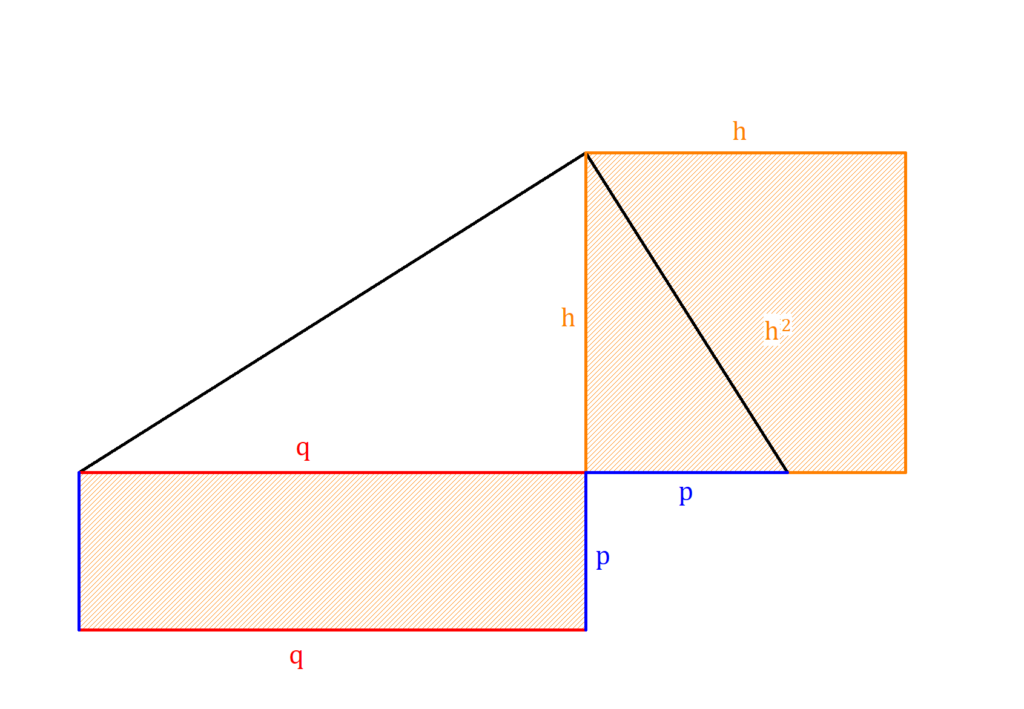
Wie funktioniert der Höhensatz : Der Höhensatz lautet:
- h2=q⋅p.
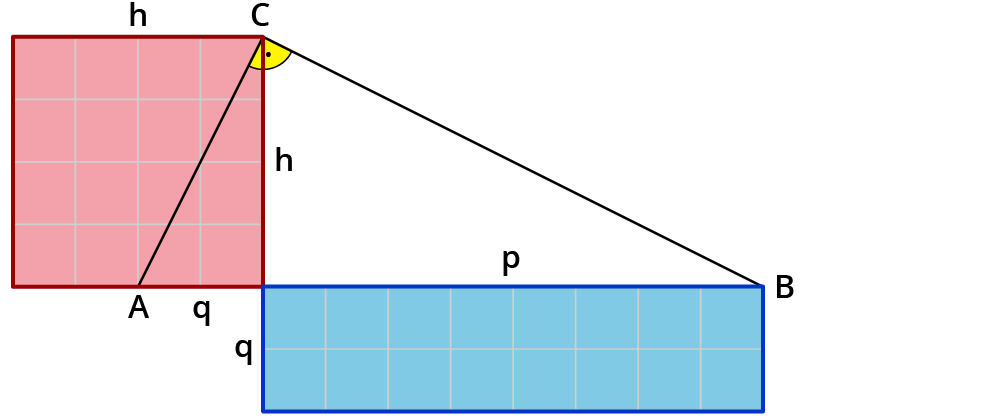
- In Worten gesprochen bedeutet der Höhensatz: Zeichnest du ein Quadrat mit der Seitenlänge h, ist das genauso groß wie der Flächeninhalt des Rechtecks mit den Seiten p und q.
- Beispiel:
- Hier ist das Quadrat mit der Seitenlänge h=4 cm eingezeichnet.
Wie berechnet man eine Kathete mit dem Satz des Pythagoras
Der Satz des Pythagoras stellt eine Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks her: Die Summe der quadrierten Katheten (a und b) ist gleich dem Quadrat der Hypotenuse (c). Die Formel a 2 + b 2 = c 2 a^2 + b^2 = c^2 a2+b2=c2 gilt nur bei rechtwinkligen Dreiecken, wenn c die Hypotenuse ist!
Wie lautet der Höhensatz Formel : Der Höhensatz des Euklid lautet h² = p · q. Das heißt, dass das Quadrat der Höhe das gleiche Ergebnis hat, wie das Produkt der Abschnitte p und q auf der Hypothenuse.
Die Satzgruppe des Pythagoras besteht aus drei Sätzen:
- Satz des Pythagoras.
- Höhensatz des Euklid.
- Kathetensatz des Euklid.
Der Flächeninhalt eines Rechtecks berechnet sich mit der Formel: A = a · b. Da man zwei Längeneinheiten multipliziert, erhält man immer eine Flächeneinheit, z.B.: cm · cm=cm2 (Man sagt: Quadratzentimeter) m · m=m2 (Man sagt: Quadratmeter)
Wie berechne ich eine Kathete mit dem Satz des Pythagoras
0:00Empfohlener Clip · 52 SekundenSatz des Pythagoras – Kathete berechnen | Mathe einfach erklärtBeginn des vorgeschlagenen ClipsEnde des vorgeschlagenen ClipsDer Satz des Pythagoras stellt eine Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks her: Die Summe der quadrierten Katheten (a und b) ist gleich dem Quadrat der Hypotenuse (c). Die Formel a 2 + b 2 = c 2 a^2 + b^2 = c^2 a2+b2=c2 gilt nur bei rechtwinkligen Dreiecken, wenn c die Hypotenuse ist!Ein rechter Winkel lässt sich auf ganz einfache Weise im Gelände abstecken. Hierzu nimmst du eine Schnur und unterteilst sie mit 11 Knoten in 12 gleich lange Teile. Mit dieser Schnur kannst du ein Dreieck mit den Seitenlängen 3, 4 und 5 legen, denn 3 + 4 + 5 = 12. Es ergibt sich ein rechter Winkel.
Flächeninhalt = → Die Hypotenuse c wird durch die Höhe in die Abschnitte q und p geteilt → c = q + p → In rechtwinkligen Dreiecken gilt der Satz des Pythagoras → In einem rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den beiden Katheten.
Wie kann man den Satz des Pythagoras beweisen : Satz des Pythagoras: Beweis
Ziehe die Flächen des großen Quadrates in die kleinen hinein, indem du mit der Maus auf die roten Punkte klickst, gedrückt hältst und bewegst. Du kannst außerdem die Lage des Punktes C verändern, was zeigt, dass der Satz des Pythagoras wirklich in allen rechtwinkligen Dreiecken gilt!
Was wird mit der Formel 2 * R * Pi berechnet : Mit Hilfe der Formel für den Umfang des Kreises U = 2 π r kannst du eine Formel für den Flächeninhalt des Kreises herleiten. Aus den Kreisteilen lässt sich ein angenähertes Rechteck legen.
Was ist die Umfangsformel
Du zählst zweimal die Länge a und zweimal die Breite b zusammen. Um den Rechteck Umfang zu berechnen, addierst du die Längen aller Seiten miteinander. Die Umfang Formel ist also U = 2 · a + 2 · b.
a² + b² = c² .
- Wenn die fehlende Seite a ist, musst du die Gleichung so umwandeln, dass a alleine auf einer Seite steht, und die Quadratwurzel ziehen: a = √(c² – b²) ,
- wenn die Seite b unbekannt ist, dann: b = √(c² – a²) und.
- wenn die Hypotenuse c gesucht wird, lautet die Formel: c = √(a² + b²) .
Winkel mit einem Zollstock messen
- Klappen Sie die vorderen beiden, aufeinanderfolgenden Glieder Ihres Zollstocks so zusammen, dass ein Dreieck entsteht.
- Die Kante des Zollstockanfangs sollte auf 67,7 Zentimeter (cm) gerichtet sein.
- Dadurch erhalten Sie am oberen Ende des Dreiecks einen 90-Grad-Winkel.
Was bedeutet 67 7 cm auf dem Zollstock : Mit einem Zollstock einen 90° Winkel definieren
Knicke die ersten beiden Glieder so, dass das erste Glied auf 67,7 cm zeigt. Achte darauf, dass die Spitze des Metallgliedes auf die 67,7 cm zeigt und nicht die Holzspitze.