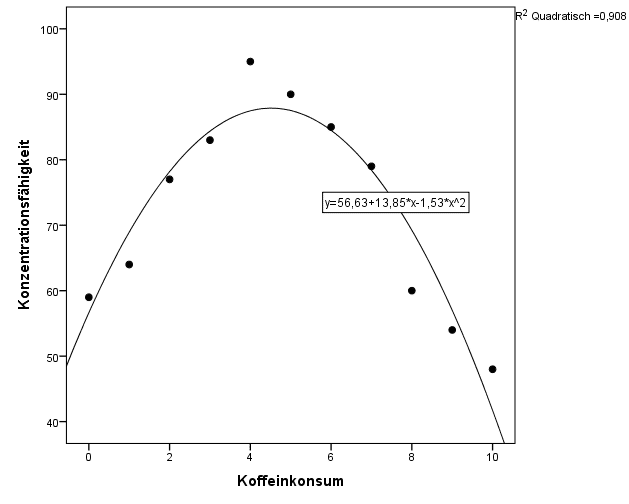
Nichtlineare Funktionen sind alle Funktionen, die sich nicht in der Form f(x) = ax + b schreiben lassen. Alle quadratischen oder Polynome höheren Grades sind nichtlinear.Die Punktprobe bei linearen Funktionen
Dazu setzt man die Koordinaten des Punktes in die Funktionsgleichung ein und prüft, ob man eine wahre oder eine falsche Aussage erhält. Ist die Aussage wahr, liegt der Punkt auf der Geraden, andernfalls nicht.Beispiele für nichtlineare Gleichungen
Nichtlineare Gleichungen ergeben grafisch abgebildet keine Geraden (die überall dieselbe Steigung haben), sondern sind „kurvig“, beispielsweise Parabeln, die an unterschiedlichen Stellen / Punkten unterschiedliche Steigungen haben.
Wie sieht linear aus : Funktionsgleichungen linearer Funktionen bestimmen
Eine lineare Funktion hat die allgemeine Form f(x)=m⋅x+t. Dabei gilt: m bezeichnet die Steigung der Funktion. t bezeichnet den y-Achsenabschnitt, also den Schnittpunkt des Graphen mit der y-Achse.
Wann ist es linear
Bei einer linearen Funktion ist die Steigung m an jeder Stelle gleich. Wenn gilt, dann steigt die lineare Funktion, verläuft also von links oben nach rechts unten. Wenn gilt, dann fällt die lineare Funktion, verläuft also von rechts oben nach links unten.
Wann ist etwas linear : Eine Funktion f : R → R heißt linear, wenn sie von der Form x ↦→ a + bx mit festen reellen Zahlen a, b ist. Ist b = 0, also f(x) = a für alle x ∈ R, so nennt man f eine konstante Funktion (mit Wert a).
linear (sequential):
geradlinig.
Eine lineare Gleichung ist eine Gleichung, in der alle Variablen „linear“, d. h. in der ersten Potenz vorkommen. Eine lineare Gleichung mit einer Variablen hat immer entweder genau eine oder keine Lösung.
Wann ist eine lineare Gleichung linear
Die Gleichung einer linearen Funktion hat immer die Gestalt y=mx+b. Sie wird auch Normalform der Geradengleichung genannt. Dabei ist m die Steigung und b der y-Achsenabschnitt der Funktion. Im Fall y=2xist die Steigung m = 2 und der y-Achsenabschnitt b = 0.Im Fall y=2x-2ist die Steigung ebenfalls m = 2.Allgemeine Definition
Linearität ist die Eigenschaft eines Systems, auf die Veränderung eines Parameters stets mit einer dazu proportionalen Änderung eines anderen Parameters zu reagieren. Diese allgemeine Definition trifft gleichermaßen für Mathematik, Naturwissenschaft und Technik zu.nichtlinear. Bedeutungen: [1] nicht in Form einer Linie verlaufend. [2] nicht in einer Richtung stetig verlaufend, mit Abschweifung.
Linearen Funktionen: Definition
Lineare Funktionen beschreiben immer ein lineares Verhältnis, bzw. eine lineare Zuordnung zwischen zwei Variablen. Daher sind ihre Graphen eine gerade Linie im Koordinatensystem.
Warum heisst es linear : Der Begriff linear leitet sich von lateinisch linea = "Leine, Schnur, Faden" ab. Der Graph einer linearen Funktion ist sozusagen eine "gespannte Leine", also eine Gerade. Den Graphen einer linearen Funktion kannst du von den Graphen anderer Funktionen unterscheiden.
Wann ist linear : im zweidimensionalen Raum: Vektoren sind linear abhängig, wenn sie in die gleiche Richtung zeigen. Das heißt, jeder der Vektoren lässt sich mithilfe der skalaren Multiplikation als ein Vielfaches der anderen Vektoren darstellen.
Welche Gleichungen sind linear
Eine lineare Gleichung ist eine Gleichung, in der alle Variablen „linear“, d. h. in der ersten Potenz vorkommen. Eine lineare Gleichung mit einer Variablen hat immer entweder genau eine oder keine Lösung.
Merkmale des linearen Mindsets:
Zusammenhänge gelten als linear und eindeutig kausal. Systeme und Probleme werden separiert betrachtet. Vernetzte, komplexe Zusammenhänge werden nicht erfasst und ohne Kenntnis der Wechselwirkungen beurteilt. Nur Bekanntes wird wahrgenommen und bei Planungen und Prognosen einbezogen.Die lineare Funktion ist eine Funktion, deren Funktionsgraph eine Linie ist. Etwas mathematischer ausgedrückt, heißen diese Linien Geraden. Eine lineare Funktionsgleichung sieht allgemein so aus: f ( x ) = m ⋅ x + b f(x)=m\cdot x+b f(x)=m⋅x+b.
Was heißt linear auf Deutsch : linear (sequential):
geradlinig.